الگوریتم ژنتیک
الگوریتمهای ژنتیک (به انگلیسی: Genetic algorithm) تکنیک جستجو در علم رایانه برای یافتن راهحل تقریبی برای بهینهسازی مدل، ریاضی و مسائل جستجو است. الگوریتم ژنتیک نوع خاصی از الگوریتمهای تکاملی است که از تکنیکهای زیستشناسی فرگشتی مانند وراثت، جهش زیستشناسی و اصول انتخابی داروین برای یافتن فرمول بهینه جهت پیشبینی یا تطبیق الگو استفاده میشود. الگوریتمهای ژنتیک اغلب گزینه خوبی برای تکنیکهای پیشبینی بر مبنای رگرسیون هستند. در مدلسازی الگوریتم ژنتیک یک تکنیک برنامهنویسی است که از تکامل ژنتیکی به عنوان یک الگوی حل مسئله استفاده میکند. مسئلهای که باید حل شود دارای ورودیهایی میباشد که طی یک فرایند الگوبرداری شده از تکامل ژنتیکی به راهحلها تبدیل میشود سپس راه حلها به عنوان کاندیداها توسط تابع برازش یا تابع برازندگی (Fitness Function) مورد ارزیابی قرار میگیرند و چنانچه شرط خروج مسئله فراهم شده باشد الگوریتم خاتمه مییابد. بهطور کلی یک الگوریتم مبتنی بر تکرار است که اغلب بخشهای آن به صورت فرایندهای تصادفی انتخاب میشوند که این الگوریتمها از بخشهای تابع برازش، نمایش، انتخاب و تغییر تشکیل میشوند.
مقدمه
هنگامی که لغت تنازع بقا به کار میرود اغلب بار ارزشی منفی آن به ذهن میآید. شاید همزمان قانون جنگل به ذهن برسد و حکم بقای قویترها!
البته همیشه هم قویترینها برنده نبودهاند؛ مثلاً دایناسورها با وجود جثه عظیم و قویتر بودن در طی روندی کاملاً طبیعی بازیِ بقا و ادامه نسل را واگذار کردند در حالی که موجوداتی بسیار ضعیفتر از آنها حیات خویش را ادامه دادند. ظاهراً طبیعت، بهترینها را تنها بر اساس هیکل انتخاب نمیکند! در واقع درستتر آنست که بگوییم طبیعت مناسب ترینها (Fittest) را انتخاب میکند.
قانون انتخاب طبیعی بدین صورت است که تنها گونههایی از یک جمعیت ادامه نسل میدهند که بهترین خصوصیات را داشته باشند و آنهایی که این خصوصیات را نداشته باشند به تدریج و در طی زمان از بین میروند.
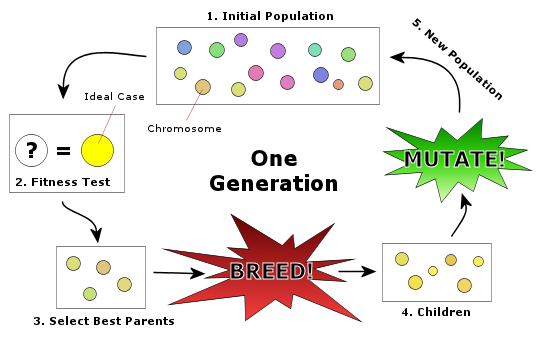
الگوریتمهای ژنتیک یکی از الگوریتمهای جستجوی تصادفی است که ایده آن برگرفته از طبیعت میباشد. الگوریتمهای ژنتیک برای روشهای کلاسیک بهینهسازی در حل مسائل خطی، محدب و برخی مشکلات مشابه بسیار موفق بودهاند ولی الگوریتمهای ژنتیک برای حل مسائل گسسته و غیر خطی بسیار کاراتر میباشند. به عنوان مثال میتوان به مسئله فروشنده دورهگرد اشاره کرد. در طبیعت از ترکیب کروموزومهای بهتر، نسلهای بهتری پدید میآیند. در این بین گاهی اوقات جهشهایی نیز در کروموزومها روی میدهد که ممکن است باعث بهتر شدن نسل بعدی شوند. الگوریتم ژنتیک نیز با استفاده از این ایده اقدام به حل مسائل میکند. روند استفاده از الگوریتمهای ژنتیک به صورت زیر میباشد:
الف) معرفی جوابهای مسئله به عنوان کروموزوم
ب) معرفی تابع برازندگی (فیت نس)
ج) جمعآوری اولین جمعیت
د) معرفی عملگرهای انتخاب
ه) معرفی عملگرهای تولید مثل
در الگوریتمهای ژنتیک ابتدا بهطور تصادفی یا الگوریتمیک، چندین جواب برای مسئله تولید میکنیم. این مجموعه جواب را جمعیت اولیه مینامیم. هر جواب را یک کروموزوم مینامیم. سپس با استفاده از عملگرهای الگوریتم ژنتیک پس از انتخاب کروموزومهای بهتر، کروموزومها را باهم ترکیب کرده و جهشی در آنها ایجاد میکنیم. در نهایت نیز جمعیت فعلی را با جمعیت جدیدی که از ترکیب و جهش در کروموزومها حاصل میشود، ترکیب میکنیم.
مثلاً فرض کنید گونه خاصی از افراد، هوش بیشتری از بقیه افرادِ یک جامعه یا کولونی دارند. در شرایط کاملاً طبیعی، این افراد پیشرفت بهتری خواهند کرد و رفاه نسبتاً بالاتری خواهند داشت و این رفاه، خود باعث طول عمر بیشتر و باروری بهتر خواهد بود (توجه کنید شرایط، طبیعیست نه در یک جامعه سطح بالا با ملاحظات امروزی؛ یعنی طول عمر بیشتر در این جامعه نمونه با زاد و ولد بیشتر همراه است). حال اگر این خصوصیت (هوش) ارثی باشد بالطبع در نسل بعدی همان جامعه تعداد افراد باهوش به دلیل زاد و ولد بیشترِ اینگونه افراد، بیشتر خواهد بود. اگر همین روند را ادامه دهید خواهید دید که در طی نسلهای متوالی دائماً جامعه نمونه ما باهوش و باهوشتر میشود. بدین ترتیب یک مکانیزم ساده طبیعی توانستهاست در طی چند نسل عملاً افراد کم هوش را از جامعه حذف کند علاوه بر اینکه میزان هوش متوسط جامعه نیز دائماً در حال افزایش است.
بدین ترتیب میتوان دید که طبیعت با بهرهگیری از یک روش بسیار ساده (حذف تدریجی گونههای نامناسب و در عین حال تکثیر بالاتر گونههای بهینه)، توانستهاست دائماً هر نسل را از لحاظ خصوصیات مختلف ارتقاء بخشد.
البته آنچه در بالا ذکر شد به تنهایی توصیفکننده آنچه واقعاً در قالب تکامل در طبیعت اتفاق میافتد نیست. بهینهسازی و تکامل تدریجی به خودی خود نمیتواند طبیعت را در دسترسی به بهترین نمونهها یاری دهد. اجازه دهید تا این مسئله را با یک مثال شرح دهیم:
پس از اختراع اتومبیل به تدریج و در طی سالها اتومبیلهای بهتری با سرعتهای بالاتر و قابلیتهای بیشتر نسبت به نمونههای اولیه تولید شدند. طبیعیست که این نمونههای متأخر حاصل تلاش مهندسان طراح جهت بهینهسازی طراحیهای قبلی بودهاند. اما دقت کنید که بهینهسازی یک اتومبیل، تنها یک «اتومبیل بهتر» را نتیجه میدهد.
اما آیا میتوان گفت اختراع هواپیما نتیجه همین تلاش بودهاست؟ یا فرضاً میتوان گفت فضاپیماها حاصل بهینهسازی طرح اولیه هواپیماها بودهاند؟
پاسخ اینست که گرچه اختراع هواپیما قطعاً تحت تأثیر دستاوردهایهای صنعت اتومبیل بودهاست؛ اما به هیچ وجه نمیتوان گفت که هواپیما صرفاً حاصل بهینهسازی اتومبیل یا فضاپیما حاصل بهینهسازی هواپیماست. در طبیعت هم عیناً همین روند حکمفرماست. گونههای متکاملتری وجود دارند که نمیتوان گفت صرفاً حاصل تکامل تدریجی گونه قبلی هستند.
در این میان آنچه شاید بتواند تا حدودی ما را در فهم این مسئله یاری کند مفهومیست به نام تصادف یا جهش.
به عبارتی طرح هواپیما نسبت به طرح اتومبیل یک جهش بود و نه یک حرکت تدریجی. در طبیعت نیز به همین گونهاست. در هر نسل جدید بعضی از خصوصیات به صورتی کاملاً تصادفی تغییر مییابند سپس بر اثر تکامل تدریجی که پیشتر توضیح دادیم در صورتی که این خصوصیت تصادفی شرایط طبیعت را ارضا کند حفظ میشود در غیر اینصورت به شکل اتوماتیک از چرخه طبیعت حذف میگردد.
در واقع میتوان تکامل طبیعی را به اینصورت خلاصه کرد: جستجوی کورکورانه (تصادف یا Blind Search) + بقای قویتر.
حال ببینیم که رابطه تکامل طبیعی با روشهای هوش مصنوعی چیست. هدف اصلی روشهای هوشمندِ به کار گرفته شده در هوش مصنوعی، یافتن پاسخ بهینه مسائل مهندسی است. به عنوان مثال اینکه چگونه یک موتور را طراحی کنیم تا بهترین بازدهی را داشته باشد یا چگونه بازوهای یک ربات را متحرک کنیم تا کوتاهترین مسیر را تا مقصد طی کند (دقت کنید که در صورت وجود مانع یافتن کوتاهترین مسیر دیگر به سادگی کشیدن یک خط راست بین مبدأ و مقصد نیست) همگی مسائل بهینهسازی هستند.
روشهای کلاسیک ریاضیات دارای دو اشکال اساسی هستند. اغلب این روشها نقطه بهینه محلی (Local Optima) را به عنوان نقطه بهینه کلی در نظر میگیرند و نیز هر یک از این روشها تنها برای مسئله خاصی کاربرد دارند. این دو نکته را با مثالهای سادهای روشن میکنیم.
به شکل زیر توجه کنید. این منحنی دارای دو نقطه ماکزیمم میباشد؛ که یکی از آنها تنها ماکزیمم محلی است. حال اگر از روشهای بهینهسازی ریاضی استفاده کنیم مجبوریم تا در یک بازه بسیار کوچک مقدار ماکزیمم تابع را بیابیم؛ مثلاً از نقطه ۱ شروع کنیم و تابع را ماکزیمم کنیم. بدیهی است اگر از نقطه ۱ شروع کنیم تنها به مقدار ماکزیمم محلی دست خواهیم یافت و الگوریتم ما پس از آن متوقف خواهد شد. اما در روشهای هوشمند، به ویژه الگوریتم ژنتیک به دلیل خصلت تصادفی آنها حتی اگر هم از نقطه ۱ شروع کنیم باز ممکن است در میان راه نقطه A به صورت تصادفی انتخاب شود که در این صورت ما شانس دستیابی به نقطه بهینه کلی (Global Optima) را خواهیم داشت.
در مورد نکته دوم باید بگوییم که روشهای ریاضی بهینهسازی اغلب منجر به یک فرمول یا دستورالعمل خاص برای حل هر مسئله میشوند. در حالی که روشهای هوشمند دستورالعملهایی هستند که به صورت کلی میتوانند در حل هر مسئلهای به کار گرفته شوند. این نکته را پس از آشنایی با خود الگوریتم بیشتر و بهتر خواهید دید.
نحوه عملکرد الگوریتم ژنتیک روش کار الگوریتم ژنتیک بهطور فریبندهای ساده، قابل درک و بهطور قابل ملاحظهای روشی است که ما معتقدیم حیوانات آنگونه تکامل یافتهاند. هر فرمولی که از طرح داده شده بالا تبعیت کند فردی از جمعیت فرمولهای ممکن تلقی میشود. الگوریتم ژنتیک در انسان متغیرهایی که هر فرمول دادهشده را مشخص میکنند به عنوان یکسری از اعداد نشان دادهشدهاند که معادل DNA آن فرد را تشکیل میدهند. موتور الگوریتم ژنتیک یک جمعیت اولیه اینگونه است که هر فرد در برابر مجموعهای از دادهها مورد آزمایش قرار میگیرد و مناسبترین آنها باقی میمانند؛ بقیه کنار گذاشته میشوند. مناسبترین افراد با هم جفتگیری (جابجایی عناصر DNA) و (تغییر تصادفی عناصر DNA) کرده و مشاهده میشود که با گذشت از میان تعداد زیادی از نسلها، الگوریتم ژنتیک به سمت ایجاد فرمولهایی که دقیقتر هستند، میل میکنند. در فرمول نهایی برای کاربر انسانی قابل مشاهده خواهد بوده و برای ارائه سطح اطمینان نتایج میتوان تکنیکهای آماری متعارف را بر روی این فرمولها اعمال کرد که در نتیجه جمعیت را کلاً قویتر میسازند. الگوریتم ژنتیک درمدل سازی مختصراً گفته میشود که الگوریتم ژنتیک یک تکنیک برنامهنویسی است که از تکامل ژنتیکی به عنوان یک الگوی حل مسئله استفاده میکند. مسئلهای که باید حل شود دارای ورودیهایی میباشد که طی یک فرایند الگو برداری شده از تکامل ژنتیکی به راه حلها تبدیل سپس راه حلها به عنوان کاندید توسط تابع ارزیاب (fitness function) مورد ارزیابی قرار گرفته و چنانچه شرط خروج مسئله فراهم باشد الگوریتم خاتمه مییابد. در هر نسل، مناسبترینها انتخاب میشوند نه بهترینها. یک راهحل برای مسئله مورد نظر، با یک لیست از پارامترها نشان داده میشود که به آنها کروموزوم یا ژنوم میگویند. کروموزومها عموماً به صورت یک رشته ساده از دادهها نمایش داده میشوند، البته انواع ساختمان دادههای دیگر هم میتوانند مورد استفاده قرار گیرند. در ابتدا چندین مشخصه به صورت تصادفی برای ایجاد نسل اول تولید میشوند. در طول هر نسل، هر مشخصه ارزیابی میشود و ارزش تناسب (fitness) توسط تابع تناسب اندازهگیری میشود.
گام بعدی ایجاد دومین نسل از جامعه است که بر پایه فرایندهای انتخاب، تولید از روی مشخصههای انتخاب شده با عملگرهای ژنتیکی است: اتصال کروموزومها به سر یکدیگر و تغییر.
برای هر فرد، یک جفت والد انتخاب میشود. انتخابها به گونهایاند که مناسبترین عناصر انتخاب شوند تا حتی ضعیفترین عناصر هم شانس انتخاب داشته باشند تا از نزدیک شدن به جواب محلی جلوگیری شود. چندین الگوی انتخاب وجود دارد: چرخ منگنهدار (رولت)، انتخاب مسابقهای (Tournament) ،... .
معمولاً الگوریتمهای ژنتیک یک عدد احتمال اتصال دارد که بین ۰٫۶ و ۱ است که احتمال به وجود آمدن فرزند را نشان میدهد. ارگانیسمها با این احتمال دوباره با هم ترکیب میشوند. اتصال ۲ کروموزوم فرزند ایجاد میکند، که به نسل بعدی اضافه میشوند. این کارها انجام میشوند تا این که کاندیدهای مناسبی برای جواب، در نسل بعدی پیدا شوند. مرحله بعدی تغییر دادن فرزندان جدید است. الگوریتمهای ژنتیک یک احتمال تغییر کوچک و ثابت دارند که معمولاً درجهای در حدود ۰٫۰۱ یا کمتر دارد. بر اساس این احتمال، کروموزومهای فرزند بهطور تصادفی تغییر میکنند یا جهش مییابند، مخصوصاً با جهش بیتها در کروموزوم ساختمان دادهمان.
این فرایند باعث به وجود آمدن نسل جدیدی از کروموزومهایی میشود، که با نسل قبلی متفاوت است. کل فرایند برای نسل بعدی هم تکرار میشود، جفتها برای ترکیب انتخاب میشوند، جمعیت نسل سوم به وجود میآیند و … این فرایند تکرار میشود تا این که به آخرین مرحله برسیم.
شرایط خاتمه الگوریتمهای ژنتیک عبارتند از:
- به تعداد ثابتی از نسلها برسیم.
- بودجه اختصاص دادهشده تمام شود (زمان محاسبه/پول).
- یک فرد (فرزند تولید شده) پیدا شود که مینیمم (کمترین) ملاک را برآورده کند.
- بیشترین درجه برازش فرزندان حاصل شود یا دیگر نتایج بهتری حاصل نشود.
- بازرسی دستی.
- ترکیبهای بالا.
روشهای نمایش
قبل از این که یک الگوریتم ژنتیک برای یک مسئله اجرا شود، یک روش برای کد کردن ژنومها به زبان کامپیوتر باید به کار رود. یکی از روشهای معمول کد کردن به صورت رشتههای باینری است: رشتههای ۰ و ۱. یک راه حل مشابه دیگر کد کردن راه حلها در آرایهای از اعداد صحیح یا اعداد اعشاری است. سومین روش برای نمایش صفات در یک GA یک رشته از حروف است، که هر حرف دوباره نمایش دهنده یک خصوصیت از راه حل است. خاصیت هر سه روش این است که آنها تعریف سازندهای را که تغییرات تصادفی در آنها ایجاد میکنند را آسان میکنند: ۰ را به ۱ و برعکس، اضافه یا کم کردن ارزش یک عدد یا تبدیل یک به صفر یا برعکس. یک روش دیگر که توسط John Koza توسعه یافت، برنامهنویسی ژنتیک است؛ که برنامهها را به عنوان شاخههای داده در ساختار درخت نشان میدهد. در این روش تغییرات تصادفی میتوانند با عوض کردن عملگرها یا تغییر دادن ارزش یک گره داده شده در درخت، یا عوض کردن یک زیر درخت با دیگری به وجود آیند.
عملگرهای یک الگوریتم ژنتیک
در هر مسئله قبل از آنکه بتوان الگوریتم ژنتیک را برای یافتن یک پاسخ به کار برد به دو عنصر نیاز است:در ابتدا روشی برای ارائه یک جواب به شکلی که الگوریتم ژنتیک بتواند روی آن عمل کند لازم است. در دومین جزء اساسی الگوریتم ژنتیک روشی است که بتواند کیفیت هر جواب پیشنهاد شده را با استفاده از توابع تناسب محاسبه نماید.
شبه کد
1 Genetic Algorithm 2 begin 3 Choose initial population 4 repeat 5 Evaluate the individual fitness of a certain proportion of the population 6 Select pairs of best-ranking individuals to reproduce 7 Apply crossover operator 8 Apply mutation operator 9 until terminating condition 10 end
شمای کلی شبه کد 
ایده اصلی
در دهه هفتاد میلادی دانشمندی از دانشگاه میشیگان به نام جان هلند ایده استفاده از الگوریتم ژنتیک را در بهینهسازیهای مهندسی مطرح کرد. ایده اساسی این الگوریتم انتقال خصوصیات موروثی توسط ژنهاست. فرض کنید مجموعه خصوصیات انسان توسط کروموزومهای او به نسل بعدی منتقل میشوند. هر ژن در این کروموزومها نماینده یک خصوصیت است. به عنوان مثال ژن ۱ میتواند رنگ چشم باشد، ژن ۲ طول قد، ژن ۳ رنگ مو و الی آخر. حال اگر این کروموزوم به تمامی، به نسل بعد انتقال یابد، تمامی خصوصیات نسل بعدی شبیه به خصوصیات نسل قبل خواهد بود. بدیهیست که در عمل چنین اتفاقی رخ نمیدهد. در واقع به صورت همزمان دو اتفاق برای کروموزومها میافتد. اتفاق اول جهش (Mutation) است. «جهش» به این صورت است که بعضی ژنها به صورت کاملاً تصادفی تغییر میکنند. البته تعداد اینگونه ژنها بسیار کم میباشد اما در هر حال این تغییر تصادفی همانگونه که پیشتر دیدیم بسیار مهم است؛ مثلاً ژن رنگ چشم میتواند به صورت تصادفی باعث شود تا در نسل بعدی یک نفر دارای چشمان سبز باشد. در حالی که تمامی نسل قبل دارای چشم قهوهای بودهاند. علاوه بر «جهش» اتفاق دیگری که میافتد و البته این اتفاق به تعداد بسیار بیشتری نسبت به «جهش» رخ میدهد چسبیدن دو کروموزوم از طول به یکدیگر و تبادل برخی قطعات بین دو کروموزوم است. این مسئله با نام Crossover شناخته میشود. این همان چیزیست که باعث میشود تا فرزندان ترکیب ژنهای متفاوتی را (نسبت به والدین خود) به فرزندان خود انتقال دهند.
روشهای انتخاب
روشهای مختلفی برای الگوریتمهای ژنتیک وجود دارند که میتوان برای انتخاب ژنومها از آنها استفاده کرد. اما روشهای لیست شده در پایین از معمولترین روشها هستند.
انتخاب Elitist
مناسبترین عضو هر اجتماع انتخاب میشود.
انتخاب Roulette
یک روش انتخاب است که در آن عنصری که عدد برازش (تناسب) بیشتری داشته باشد، انتخاب میشود. در واقع به نسبت عدد برازش برای هر عنصر یک احتمال تجمعی نسبت میدهیم و با این احتمال است که شانس انتخاب هر عنصر تعیین میشود.
انتخاب Scaling
به موازات افزایش متوسط عدد برازش جامعه، سنگینی انتخاب هم بیشتر میشود و جزئیتر. این روش وقتی کاربرد دارد که مجموعه دارای عناصری باشد که عدد برازش بزرگی دارند و فقط تفاوتهای کوچکی آنها را از هم تفکیک میکند.
انتخاب Tournament
یک زیر مجموعه از صفات یک جامعه انتخاب میشوند و اعضای آن مجموعه با هم رقابت میکنند و سرانجام فقط یک صفت از هر زیرگروه برای تولید انتخاب میشوند.
بعضی از روشهای دیگر عبارتند از:
مثال عملی
در این مثال میخواهیم مسئلهٔ ۸ وزیر را بوسیلهٔ این الگوریتم حل کنیم. هدف مشخص کردن چیدمانی از ۸ وزیر در صفحهٔ شطرنج است به نحوی که هیچیک همدیگر را تهدید نکند. ابتدا باید نسل اولیه را تولید کنیم. صفحه شطرنج ۸ در ۸ را در نظر بگیرید. ستونها را با اعداد ۰ تا ۷ و سطرها را هم از ۰ تا ۷ مشخص میکنیم. برای تولید حالات (کروموزومها) اولیه به صورت تصادفی وزیرها را در ستونهای مختلف قرار میدهیم. باید در نظر داشت که وجود نسل اولیه با شرایط بهتر سرعت رسیدن به جواب را افزایش میدهد (اصالت نژاد) به همین خاطر وزیر i ام را در خانهٔ تصادفی در ستون i ام قرار میدهیم (به جای اینکه هر مهرهای بتواند در هر خانه خالی قرار بگیرد). با اینکار حداقل از برخورد ستونی وزیرها جلوگیری میشود. توضیح بیشتر اینکه مثلاً وزیر اول را بهطور تصادفی در خانههای ستون اول که با ۰ مشخص شده قرار میدهیم تا به آخر. i=۰٬۱، … ۷ حال باید این حالت را به نحوی کمی مدل کرد. چون در هر ستون یک وزیر قرار دادیم هر حالت را بوسیلهٔ رشته اعدادی که عدد k ام در این رشته شمارهٔ سطر وزیر موجود در ستون i ام را نشان میدهد؛ یعنی یک حالت که انتخاب کردیم میتواند به صورت زیر باشد: ۶۷۲۰۳۴۲۲ که ۶ شمارهٔ سطر ۶ است که وزیر اول که شمارهٔ ستونش ۰ است میباشد تا آخر. فرض کنید ۴ حالت زیر به تصادف تولید شدهاند. این چهار حالت را به عنوان کروموزومهای اولیه بکار میگیریم.
- ) ۶۷۲۰۳۴۲۰
- ) ۷۰۰۶۳۳۵۴
- ) ۱۷۵۲۲۰۶۳
- )۴۳۶۰۲۴۷۱
حال نوبت به تابع برازش fitness function میرسد. تابعی را که در نظر میگیریم تابعی است که برای هر حالت تعداد برخوردها (تهدیدها) را در نظر میگیرد. هدف صفر کردن یا حداقل کردن این تابع است. پس احتمال انتخاب کروموزومی برای تولید نسل بیشتر است که مقدار محاسبه شده توسط تابع برازش برای آن کمتر باشد. (روشهای دیگری نیز برای انتخاب وجود دارد) مقدار برازش برای حالات اولیه به صورت زیر میباشد: (مقدار عدد برازش در جلوی هر کروموزوم (با رنگ قرمز)همان تعداد برخوردهای وزیران میباشد)
- )۶۷۲۰۳۴۲۰ ← ۶
- )۷۰۰۶۳۳۵۴ ← ۸
- )۱۷۵۲۲۰۶۳ ← ۲
- )۴۳۶۰۲۴۷۱ ← ۴
پس احتمالها به صورت زیر است:

در اینجا کروموزومهایی را انتخاب میکنیم که برازندگی کمتری دارند. پس کروموزوم ۳ برای crossover با کروموزومهای ۴ و ۱ انتخاب میشود. نقطهٔ ترکیب را بین ارقام ۶ و ۷ در نظر میگیریم.
۴ و ۳:
- )۱۷۵۲۲۰۷۱
- )۴۳۶۰۲۴۶۳
۱ و ۳:
- )۱۷۵۲۲۰۲۰
- )۶۷۲۰۳۴۶۳
حال نوبت به جهش میرسد. در جهش باید یکی از ژنها تغییر کند.
فرض کنید از بین کروموزومهای ۵ تا ۸ کروموزوم شمارهٔ ۷ و از بین ژن چهارم از ۲ به ۳ جهش یابد. پس نسل ما شامل کروموزومهای زیر با امتیازات نشان داده شده میباشد: (امتیازات تعداد برخوردها میباشد)
- )۶۷۲۰۳۴۲۰ ← ۶
- )۷۰۰۶۳۳۵۴ ← ۸
- )۱۷۵۲۲۰۶۳ ← ۲
- )۴۳۶۰۲۴۷۱ ← ۴
- )۱۷۵۲۲۰۷۱ ← ۶
- )۴۳۶۰۲۴۶۳ ← ۴
- )۱۷۵۳۲۰۲۰ ← ۴
- )۶۷۲۰۳۴۶۳ ← ۵
کروموزوم ۳ کاندیدای خوبی برای ترکیب با ۶ و ۷ میباشد. (فرض در این مرحله جهشی صورت نگیرد و نقطهٔ اتصال بین ژنهای ۱ و ۲ باشد)
- )۶۷۲۰۳۴۲۰ ← ۶
- )۷۰۰۶۳۳۵۴ ← ۸
- )۱۷۵۲۲۰۶۳ ← ۲
- )۴۳۶۰۲۴۷۱ ← ۴
- )۱۷۵۲۲۰۷۱ ← ۶
- )۴۳۶۰۲۴۶۳ ← ۴
- )۱۷۵۳۲۰۳۰ ← ۴
- )۶۷۲۰۳۴۶۳ ← ۵
- )۱۳۶۰۲۴۶۳ ← ۲
- )۴۷۵۲۲۰۶۳ ← ۲
- )۱۷۵۲۲۰۲۰ ← ۴
- )۱۷۵۲۲۰۶۳ ← ۲
کروموزومهای از ۹ تا ۱۲ را نسل جدید میگوییم. بهطور مشخص کروموزومهای تولید شده در نسل جدید به جواب مسئله نزدیکتر شدهاند. با ادامهٔ همین روند پس از چند مرحله به جواب مورد نظر خواهیم رسید.
روش جستجوی تکاملی
روشهای جستجوی ناآگاهانه، آگاهانه و فراابتکاری (به انگلیسی: Metaheuristic) برای حل مسائل هوش مصنوعی بسیار کارآمد میباشند. در مورد مسائل بهینهسازی اغلب روشهای آگاهانه و ناآگاهانه جوابگوی نیاز نخواهند بود چرا که بیشتر مسائل بهینهسازی در رده مسائل NP قرار دارند؛ بنابراین نیاز به روش جستجوی دیگری وجود دارد که بتواند در فضای حالت مسائل NP به طرف جواب بهینه سراسری حرکت کند. بدین منظور روشهای جستجوی فراابتکاری مطرح میشوند، این روشهای جستجو میتوانند به سمت بهینگیهای سراسری مسئله حرکت کنند. در کنار روشهای جستجوی فراابتکاری، روشهای جستجوی دیگری نیز وجود دارند که به روشهای تکاملی معروفند.
نظریه تکامل
بر اساس نظریه تکامل داروین نسلهایی که از ویژگیهای و خصوصیات برتری نسبت به نسلهای دیگر برخوردارند شانس بیشتری نیز برای بقا و تکثیر خواهند داشت و ویژگیها و خصوصیات برتر آنها به نسلهای بعدی آنان نیز منتقل خواهد شد. همچنین بخش دوم نظریه داروین بیان میکند که هنگام تکثیر یک ارگان فرزند، به تصادف رویدادهایی اتفاق میافتد که موجب تغییر خصوصیات ارگان فرزند میشود و در صورتی که این تغییر فایدهای برای ارگان فرزند داشته باشد موجب افزایش احتمال بقای آن ارگان فرزند خواهد شد. در محاسبات کامپیوتری، بر اساس این نظریه داروین روشهایی برای مسائل بهینهسازی مطرح شدند که همه این روشها از پردازش تکاملی در طبیعت نشات گرفتهاند. به روشهای جستجو، الگوریتمهای جستجوی تکاملی گفته میشود.
انواع مختلف الگوریتمهای تکاملی
انواع مختلف الگوریتمهای تکاملی که تا به حال مطرح شدهاند، به شرح زیر میباشد:
الگوریتم ژنتیک
کدگذاری و نحوه نمایش
نحوه نمایش جواب مسئله و ژنها در موفقیت الگوریتم و نحوه پیادهسازی الگوریتم ژنتیک تأثیر بسیار مهمی دارد. در بیشتر مسائل نیز روشهای مختلفی برای نشان دادن جواب مسئله میتوان طراحی کرد.
حل مسائل معروف با استفاده از الگوریتم ژنتیک
یکی از مسائل کلاسیک در الگوریتمهای ژنتیک مسئله ۸ وزیر است. ماهیت مسئله به گونهای است که مدلسازی آن و همچنین اعمال عملگرهای الگوریتم ژنتیک بر روی آن بسیار ساده است. همچنین علاوه برای الگوریتم ژنتیک، روش الگوریتم تبرید شبیهسازی شده نیز در سادهترین شکل خود برای مسئله چند وزیر نیز روش مناسبی هست همچنین از مسائل مهم دیگری که با استفاده از این الگوریتم قابل حل میباشد مسئلهٔ فروشندهٔ دورهگرد یا مسئلهٔ چیدمان دینامیک میباشد.
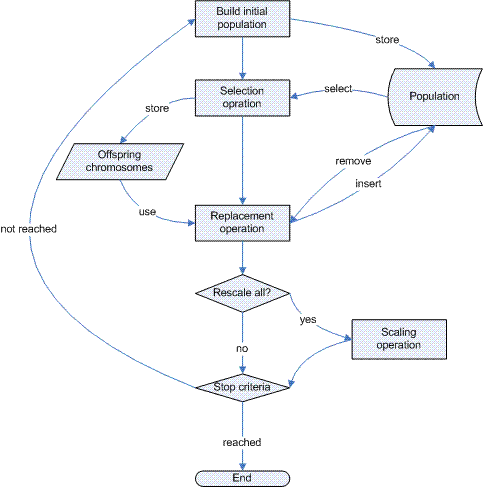
فلو چارت این الگوریتم
- مقاله علمی 2022 جهت مطالعه بیشتر:
Panahizadeh, V., Ghasemi, A.H., Dadgar Asl, Y. and Davoudi, M. (2022), "Optimization of LB-PBF process parameters to achieve best relative density and surface roughness for Ti6Al4V samples: using NSGA-II algorithm", Rapid Prototyping Journal, Vol. 28 No. 9, pp. 1821-1833.
https://doi.org/10.1108/RPJ-09-2021-0238
هدف این مقاله بررسی توانایی الگوریتم ژنتیک چندهدفه در تعیین پارامتر فرآیند و شرایط پس از فرآیند است که منجر به حداکثر چگالی نسبی (RD) و حداقل زبری سطح (Ra) به طور همزمان در مورد فرآیند نمونه Ti6Al4V توسط همجوشی بستر پودر پرتو لیزر میشود.
جستارهای وابسته
- نظامالدین فقیه، توازن خط تولید با الگوریتم ژنتیک ۹۷۸-۹۶۴-۳۵۸-۷۷۲-۷:شابک
- نظامالدین فقیه، الگوریتم ژنتیک در برنامهریزی ۹۶۴-۸۵۶۹-۱۹-۳:شابک
- کورش عشقی؛ مهدی کریمی نسب؛ تحلیل الگوریتمها و طراحی روشهای فراابتکاری؛ انتشارات دانشگاه شریف؛ ۱۳۹۵
- An introduction to genetic algorithms by Melanie Mitchell - Computers - 1998 - 209 pages
- Mitchell, Melanie, (1996), An Introduction to Genetic Algorithms, MIT Press, Cambridge, MA.
- Genetic Algorithms in Search, Optimization, and Machine Learning by David E. Goldberg (very useful)
- Holland, John H (1975), Adaptation in Natural and Artificial Systems, University of Michigan Press, Ann Arbor
- Koza, John (1992), Genetic Programming: On the Programming of Computers by Means of Natural Selection, MIT Press. ISBN 0-262-11170-5
- Michalewicz, Zbigniew (1999), Genetic Algorithms + Data Structures = Evolution Programs, Springer-Verlag.
- Mitchell, Melanie, (1996), An Introduction to Genetic Algorithms, MIT Press, Cambridge, MA.
- Poli, R. , Langdon, W. B. , McPhee, N. F. (2008). A Field Guide to Genetic Programming. Lulu.com, freely a
- ویکیپدیای انگلیسی:
- Goldberg, David E (1989), Genetic Algorithms in Search, Optimization and Machine Learning, Kluwer Academic Publishers, Boston, MA.
- Goldberg, David E (2002), The Design of Innovation: Lessons from and for Competent Genetic Algorithms, Addison-Wesley, Reading, MA.
- Fogel, David B (2006), Evolutionary Computation: Toward a New Philosophy of Machine Intelligence, IEEE Press, Piscataway, NJ. Third Edition
- Holland, John H (1975), Adaptation in Natural and Artificial Systems, University of Michigan Press, Ann Arbor
- Koza, John (1992), Genetic Programming: On the Programming of Computers by Means of Natural Selection, انتشارات امآیتی. شابک ۰−۲۶۲−۱۱۱۷۰−۵
- Michalewicz, Zbigniew (1999), Genetic Algorithms + Data Structures = Evolution Programs, Springer-Verlag.
- Mitchell, Melanie, (1996), An Introduction to Genetic Algorithms, MIT Press, Cambridge, MA.
-
Poli, R. , Langdon, W. B. , McPhee, N. F. (2008), A Field Guide to Genetic Programming (به انگلیسی), Lulu.com freely available from the internet
{{citation}}: نگهداری یادکرد:نامهای متعدد:فهرست نویسندگان (link) - Rechenberg, Ingo (1971): Evolutionsstrategie - Optimierung technischer Systeme nach Prinzipien der biologischen Evolution (PhD thesis). Reprinted by Fromman-Holzboog (1973).
- Schmitt, Lothar M, Nehaniv Chrystopher N, Fujii Robert H (1998), Linear analysis of genetic algorithms, Theoretical Computer Science (208), pp. 111–148
- Schmitt, Lothar M (2001), Theory of Genetic Algorithms, Theoretical Computer Science (259), pp. 1–61
- Schmitt, Lothar M (2004), Theory of Genetic Algorithms II: models for genetic operators over the string-tensor representation of populations and convergence to global optima for arbitrary fitness function under scaling, Theoretical Computer Science (310), pp. 181–231
- Schwefel, Hans-Paul (1974): Numerische Optimierung von Computer-Modellen (PhD thesis). Reprinted by Birkhäuser (1977).
- Vose, Michael D (1999), The Simple Genetic Algorithm: Foundations and Theory, MIT Press, Cambridge, MA.
- Whitley, D. (1994). A genetic algorithm tutorial. Statistics and Computing 4, 65–85.