الگوریتم هیرشبرگ

در علوم رایانه، الگوریتم هیرشبرگ (به انگلیسی: Hirschberg's Algorithm) الگوریتمی برای هم‌ترازسازی بهینهٔ دو توالی است که دان هیرشبرگ (Dan Hirschberg) در سال ۱۹۷۵ آن را ارائه کرد.

مقالهٔ دان هیرشبرگ که در سال ۱۹۷۵ منتشر شد.

در این الگوریتم برای ارزیابی هم‌ترازی‌ها از فاصله لون‌اشتاین استفاده می‌شود؛ در هم‌ترازی بهینه مجموع هزینه‌های درج، حذف و جایگزین‌کردن حروف برای یکسان‌کردن دو رشته، کمینهٔ تمام هم‌ترازی‌های ممکن است.

الگوریتم نیدلمن-وانچ یکی از اولین الگوریتم‌هایی است که برای هم‌ترازسازی سراسری دو توالی از برنامه‌نویسی پویا استفاده می‌کند. الگوریتم هیرشبرگ در واقع نسخه‌ای از الگوریتم نیدلمن-وانچ است که با تقسیم و حل مسئله را حل می‌کند و مصرف حافظهٔ بهینه‌تری دارد.

ایده‌های اصلی

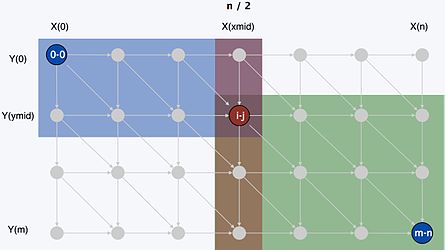
هوشمندی الگوریتم هیرشبرگ در استفاده از مشاهده‌های زیر است:

1. برای محاسبهٔ امتیاز (یا فاصله‌ی) بهینهٔ هم‌ترازی، کافی است سطر قبلی و سطر جاری را ذخیره کرد (و نه کل سطور ماتریس امتیاز نیدلمن-وانچ).
2. اگر ${\displaystyle (Z,W)=OptAlign(X,Y)}$هم‌ترازی سراسری بهینهٔ رشتههای X و Y باشد و ${\displaystyle X=X^{l}+X^{r}}$تقسیم‌بندی دلخواهی از X باشد، تقسیم‌بندی ${\displaystyle Y=Y^{l}+Y^{r}}$از Y وجود دارد که ${\displaystyle (Z,W)=OptAlign(X^{l},Y^{l})+OptAlign(X^{r},Y^{r})}$.

این الگوریتم از ایدهٔ Savitch در نظریهٔ پیچیدگی الهام گرفته‌است.

امتیازدهی

برای محاسبهٔ امتیاز هم‌ترازی (درج و حذف، جایگزینی و تطابق) از ماتریسهای امتیازدهی استفاده می‌شود. برای مثال، در ماتریس بلوسام-۶۲, امتیاز جایگزینی آمینواسیدهای Ala و Trp، تطابق آمینواسید Ala و حذف آمینواسید Ala، به ترتیب ۳-، ۴ و ۴- است.

معمولاً برای امتیازدهی هم‌ترازی‌های آمینواسیدی (توالی‌های پروتئینی) از ماتریس‌های بلوسام یا ماتریس‌های جهش پذیرفتهٔ نقطه‌ای استفاده می‌شود.

الگوریتم

برای رشتهی مفروض ${\displaystyle X}$; ${\displaystyle X_{i}}$ حرف i ام این رشته (${\displaystyle 1\leq i\leq length(X)}$), ${\displaystyle X_{i:j}}$ زیررشتهٔ آن از حرف i ام تا j ام و ${\displaystyle rev(X)}$ رشتهٔ معکوس آن است.

برای دو حرف x و y که به ترتیب از رشتههای X و Y اند؛ امتیاز حذف x, درج y و جایگزینی x با y به ترتیب برابر ${\displaystyle Sub(x,y),Ins(y),Del(x)}$است.

تابع NWscore

شبه‌کد:

function NWscore(X,Y)
   Score(0,0) = 0
   for j=1 to length(Y)
     Score(0,j) = Score(0,j-1) + Ins(Yj)
   for i=1 to length(X)
     Score(i,0) = Score(i-1,0) + Del(Xi)
     for j=1 to length(Y)
       if( Xi == Yj ) scoreSub = Score(i-1,j-1) + Match(Xi, Yj)
       else scoreSub = Score(i-1,j-1) + Sub(Xi, Yj)
       scoreDel = Score(i-1,j) + Del(Xi)
       scoreIns = Score(i,j-1) + Ins(Yj)
       Score(i,j) = max(scoreSub, scoreDel, scoreIns)
     end
   end
   for j=0 to length(Y)
     LastLine(j) = Score(length(X),j)
   return LastLine

این تابع آخرین سطر از ماتریس امتیاز نیدلمن-وانچ را (که معمولاً با F یا score نشان داده می‌شود) در زمان ${\displaystyle O(mn)}$ و با حافظهٔ ${\displaystyle O(mn)}$ محاسبه می‌کند.

پیاده‌سازی زیر در MATLAB, با همین پیچیدگی زمانی ولی با حافظهٔ ${\displaystyle O(min\{m,n\})}$ نتیجه را محاسبه می‌کند:

function [ lastLine ] = NWscore( X, Y )

% assume length(Y) <= length(X)

    scorePrev = zeros(1, length(Y) + 1);
    lastLine = zeros(1, length(Y) + 1);

    for i = 1:length(Y)
        scorePrev(i + 1) = scorePrev(i) + Ins(Y(i));
    end

    for i = 1:length(X)
        lastLine(1) = scorePrev(1) + Del(X(i));
        for j = 1:length(Y)
            if( X(i) == Y(j) ) s1 = scorePrev(j) + Match(X(i), Y(j));
            else s1 = scorePrev(j) + Sub(X(i), Y(j));
            end
            s2 = scorePrev(j + 1) + Del(X(i));
            s3 = lastLine(j) + Ins(Y(j));
            lastLine(j + 1) = max([s1, s2, s3]);
        end
        scorePrev = lastLine;
    end

end

تابع Hirschberg

شبه‌کد:

function Hirschberg(X,Y)
   Z = ""
   W = ""
   if length(X) == 0
     for i=1 to length(Y)
       Z = Z + '-'
       W = W + Yi
     end
   else if length(Y) == 0
     for i=1 to length(X)
       Z = Z + Xi
       W = W + '-'
     end
   else if length(X) == 1 or length(Y) == 1
     (Z,W) = NW(X,Y)
   else
     xlen = length(X)
     xmid = length(X)/2
     ylen = length(Y)

     ScoreL = NWscore(X1:xmid, Y)
     ScoreR = NWscore(rev(Xxmid+1:xlen), rev(Y))
     ymid = arg max ScoreL + rev(ScoreR)

     (Z,W) = Hirschberg(X1:xmid, y1:ymid) + Hirschberg(Xxmid+1:xlen, Yymid+1:ylen)
   end
   return (Z,W)

پیاده‌سازی در MATLAB:

function [ Z, W, maxScore ] = Hirschberg( X, Y )

    if( isempty(X) )
        Z = char(ones(1, length(Y)) * '-');
        W = Y;
    elseif( isempty(Y) )
        Z = X;
        W = char(ones(1, length(X)) * '-');
    elseif( length(X) == 1 || length(Y) == 1 )
        [Z, W] = NW(X, Y);
    else
        mid1 = floor(length(X) / 2);
        s1 = NWscore(X(1:mid1), Y);
        s2 = NWscore(flip(X(mid1 + 1:end)), flip(Y));
        [maxScore, mid2] = max(s1 + flip(s2));
        mid2 = mid2 - 1;
        [temp11, temp21] = Hirschberg(X(1:mid1), Y(1:mid2));
        [temp12, temp22] = Hirschberg(X(mid1 + 1:end), Y(mid2 + 1:end));
        Z = [temp11, temp12];
        W = [temp21, temp22];
    end

end

این تابع با استفاده از روش تقسیم و حل، هم‌ترازی بهینه و امتیاز این هم‌ترازی را بدست می‌آورد. نحوهٔ پیاده‌سازی تابع NWscore بیان شد و تابع NW از الگوریتم نیدلمن-وانچ استفاده می‌کند. زمان اجرای این تابع ${\displaystyle O(mn)}$ است. دقت کنید که الگوریتم نیدلمن-وانچ در حالت کلی به ${\displaystyle O(mn)}$ حافظه نیاز دارد، اما اینجا، تنها درصورتی استفاده شده‌است که طول یکی از رشتهها (m یا n) برابر ۱ باشد و در نتیجه با مصرف حافظهٔ خطی اجرا می‌شود.

مقایسه با الگوریتم نیدلمن-وانچ

الگوریتم هیرشبرگ، مشابه الگوریتم نیدلمن-وانچ، بهترین امتیاز را با استفاده از برنامه‌نویسی پویا محاسبه کرده و هم‌ترازی متناظر با آن را می‌یابد.

پیچیدگی زمانی هم‌ترازی دو رشته با طول‌های m و n در الگوریتم هیرشبرگ ${\displaystyle O(mn)}$ (مشابه الگوریتم نیدلمن-وانچ) است.

این الگوریتم تنها ${\displaystyle O(min\{m,n\})}$حافظه نیاز دارد که بهینه‌تر از الگوریتم نیدلمن-وانچ (با حافظه ${\displaystyle O(mn)}$) است.

مثال

فرض کنید دو توالی DNA بنام‌های X و Y و امتیازهای هم‌ترازسازی به صورت زیر باشند:

${\displaystyle X=AGTACGCA,Y=TATGC}$

${\displaystyle Del(x)=-2,Ins(y)=-2,Sub(x,y)=-1,Match(x,y)=2:for\ x,y\in \{A,C,T,G\}}$

در اولین مرحلهٔ الگوریتم هیرشبرگ،${\displaystyle \operatorname {Hirschberg} (\mathrm {AGTACGCA} ,\mathrm {TATGC} )}$فراخوانده می‌شود که رشتهی X را به صورت ${\displaystyle X=\mathrm {AGTA} +\mathrm {CGCA} }$ تقسیم‌بندی می‌کند.

سپس ${\displaystyle \operatorname {NWscore} (\operatorname {rev} (\mathrm {CGCA} ),\operatorname {rev} (Y))}$فراخوانده می‌شود که حاصل آن به صورت زیر است:

       C   G   T   A   T
    0 -2  -4  -6  -8 -10
 A -2 -1  -3  -5  -4  -6
 C -4  0  -2  -4  -6  -5
 G -6 -2   2   0  -2  -4
 C -8 -4   0   1  -1  -3

و در نتیجه:

ScoreL = [ -8 -4 0 -2 -1 -3 ]
rev(ScoreR) = [ -3 -1 1 0 -4 -8 ]
Sum = [-11 -5 1 -2 -5 -11]

بیشینهٔ امتیاز در ymid = ۲ است و در نتیجه ${\displaystyle Y=\mathrm {TA} +\mathrm {TGC} }$ تقسیم‌بندی بهینهٔ Y است. به همین ترتیب در هر مرحله زیررشته‌ها تقسیم شده و هم‌ترازی بهینه بدست می‌آید. درخت زیر خلاصه‌ای از مراحل تقسیم‌بندی در این مثال را نشان می‌دهد:

               (AGTACGCA,TATGC)
               /               \
        (AGTA,TA)             (CGCA,TGC)
         /     \              /        \
     (AG, )   (TA,TA)      (CG,TG)     (CA,C)
              /   \        /   \
           (T,T) (A,A)  (C,T) (G,G)

برگ‌های این درخت، هم‌ترازی بهینه را نشان می‌دهند که به صورت زیر است:

W = AGTACGCA
Z = --TATGC-

کاربرد

معمولاً در بیوانفورماتیک از الگوریتم هیرشبرگ برای هم‌ترازسازی سراسری توالی‌های زیستی (توالی‌های آمینواسیدی و توالی‌های DNA) استفاده می‌شود. بلاست (BLAST) و فاستا (FASTA) نمونه‌های هیوریستیک استفاده از آن هستند.

پیوند به بیرون

• Dynamic Programming (توضیحات بیشتر درمورد الگوریتم هیرشبرگ و بررسی پیچیدگی زمانی آن)
• A linear space algorithm for computing maximal common subsequences بایگانی‌شده در ۲۰۱۶-۱۰-۱۴ توسط Wayback Machine