الگوریتم ناسینوف

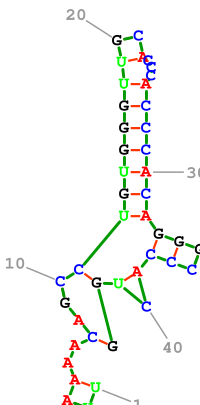
یک ساختار دوم بهینه ی توالی RNA ژنوم یک ویروس که با الگوریتم ناسینوف محاسبه شده است. ساختار 18 تا جفت باز دارد و 41 ساختار دوم مشترک بهینه (co-optimal) برای این توالی ورودی با 18 تا جفت باز وجود دارد.

الگوریتم ناسینوف (Nussinov Algorithm) حداکثر تعداد جفت بازهای ممکن یک توالی اسید نوکلئیک داده شده را محاسبه می‌کند. در مرحلهٔ بعدتر، ساختار دوم با حداکثر تعداد جفت بازها(base pair) می‌تواند ساخته شود. این الگوریتم روش‌های برنامه نویسی پویا را به کار می برد.

الگوریتم

${\displaystyle n}$ طول توالی ورودی است. N یک ماتریس ${\displaystyle n}$ در ${\displaystyle n}$ است و تابع ${\displaystyle \sigma (i,j)}$ اگر ${\displaystyle s[i]}$ مکمل ${\displaystyle s[j]}$ باشد،(یعنی باهم پیوند بازی تشکیل دهند) 1 برمی گرداند و درغیراین صورت 0 برمی گرداند. پیوندهای بازی مجاز نیستند که باهم تداخل داشته باشند. برای جفت بازهایی با اندیس‌های ${\displaystyle (a,b)}$ با شرط ${\displaystyle a<b}$ و اندیس‌های ${\displaystyle (c,d)}$ با شرط ${\displaystyle c<d}$ هیچ پیوندی ${\displaystyle a<c<b<d}$ یا ${\displaystyle c<a<d<b}$ ایجاد نمی‌شود.
زیررشتهٔ ${\displaystyle s[i..j]}$ که با ${\displaystyle s[i..i]}$ نمایش می‌شود، زیررشتهٔ به طول 1 و زیررشتهٔ ${\displaystyle s[i]}$ که با ${\displaystyle s[i..i-1]}$ نمایش داده می‌شود، زیررشتهٔ به طول 0 یا همان زیررشتهٔ تهی نامیده می‌شود.

مقداردهی اولیه

${\displaystyle N[i,i]=0,0\leq i<n}$

${\displaystyle N[i,i-1]=0,0<i<n}$

زیررشتهٔ ${\displaystyle s[i,i]}$ به طول 1 و زیررشتهٔ تهی ${\displaystyle s[i,i-1]}$ به طول 0 شامل حداکثر 0 جفت باز است.(یعنی هیچ وقت i با خودش پیوند بازی تشکیل نمی‌دهد.)

رابطهٔ بازگشتی ${\displaystyle N[i,j]=\max {\begin{Bmatrix}N[i,j-1]&\\\max _{i\leq k<j-1}(N[i,k-1]+1+N[k+1,j-1])\cdot \sigma (k,j)&\end{Bmatrix}},0\leq i<n,0<j<n,i<j}$

در انتهای الگوریتم در خانهٔ ${\displaystyle N[i,j]}$ ماتریس N ، تعداد ماکزیمم جفت بازهای زیررشته‌های ${\displaystyle s[i..j]}$ از ${\displaystyle s}$ به دست می آید. به طوری که حداکثر تعداد جفت بازهای ممکن توالی ورودی کلی ${\displaystyle s}$ در ${\displaystyle N[0,n-1]}$ ذخیره شده‌است.
موارد متمایز در رابطهٔ بازگشتی دو مورد می‌باشد . یا اینکه در زیررشتهٔ ${\displaystyle s[i..j-1]}$ حداکثر تعداد جفت بازها محاسبه شده‌است و در حال حاضر هدف گسترش آن با یک باز است که با هیچ باز دیگری جفت نشده‌است. یا به‌طور کامل تر باز ${\displaystyle s[j]}$ با یک باز دیگر در ${\displaystyle s[i..j-1]}$ پیوند تشکیل دهد. در مورد دوم k تا باز ممکن وجود دارد که ${\displaystyle s[j]}$ می‌تواند جفت باز تشکیل دهد.انتخاب باز مکمل ${\displaystyle s[j]}$، زیررشته‌های ${\displaystyle s[i.J-1]}$ را به دو زیررشتهٔ ${\displaystyle s[i.K-1]}$ و ${\displaystyle s[k+1..j-1]}$ تقسیم می‌کند و این‌ها طوری به هم وصل می‌شوند که حداکثر تعداد جفت بازها به صورت بازگشتی محاسبه شود. اگر ${\displaystyle s[k]}$ مکمل ${\displaystyle s[j]}$ باشد، مقدار تابع ${\displaystyle \sigma (k,j)}$ ، ${\displaystyle 1}$ و در غیراین صورت ${\displaystyle 0}$ است.
تمایز موارد مطابق با گرامر مستقل از متن زیر است :

${\displaystyle X=X.|X(X)|\epsilon }$

به طوریکه ${\displaystyle .}$ به یک بازِ جفت نشده(تنها) اشاره می‌کند و براکت نشان دهندهٔ همهٔ متغیرهای جفت بازهای مکمل ممکن است. پس از این گرامر همهٔ ساختارهای به دست آمده از الگوریتم ناسینوف می توانند بهینه تلقی شوند.

ساختار دوم شامل ماکزیمم تعداد پیوندهای بازی است که می توانند توسط روش برگشت به عقب از خانهٔ ${\displaystyle N[0,n-1]}$ ماتریس به دست آیند. یعنی روی ماتریس مسیرهای برگشتی وجود دارد که نتیجهٔ بهینه در ${\displaystyle N[i,n-1]}$ را می دهند و این الگوریتم برگشت به عقب عملیاتی را انجام می‌دهد که مسیرهای بهینهٔ ساختار دوم را تولید می‌کند.

کارایی

الگوریتم یک ماتریسی با ${\displaystyle n*(n+1)/2+n-1}$ درایه به کار می برد، بنابراین به ${\displaystyle O(n^{2})}$ حافظه نیاز دارد و هر درایه از طریق ${\displaystyle O(n)}$ عنصر بهینه خواهد شد پس زمان اجرای الگوریتم ${\displaystyle O(n^{3})}$ است.

علامت گذاری

مشخصات ماتریس بالا مطابق با نمایش ناسینوف بازگشتی در سال 1978 می‌باشد . گاهی اوقات به ادبیات اخیر به عنوان یک تنوعی برای این الگوریتم ناسینوف بازگشتی اشاره شده‌است(z. B. Durbin, 2006). در مقالهٔ Durbin در سال 2006 بازگشت، 4 مورد متمایز است. این گوناگونی، مقادیر محاسبه شده توسط ماتریس ${\displaystyle N}$ را تغییر نمی‌دهد، اما روش برگشت به عقب چندین مسیر مختلف در یک ساختار دوم ارائه می‌دهد که تمایز آن‌ها از نظر معنایی مبهم است.

ارتباط بیولوژیکی

ساختار دومی که شامل ماکزیمم تعداد جفت بازهاست لزوماً آن ساختاری نیست که در طبیعت (در یک سلول) اتفاق بیفتد. بنابراین در عمل الگوریتم ناسینوف برای پیش گویی ساختار دوم توالی‌های RNA به کار برده نمی‌شود. در عمل ساختار دوم پیش گویی شده تحت یک مدل ترمودینامیکی (برای مثال الگوریتم زوکر Zuker Algorithm را ببینید)است که منجر به نتایج معنادار بیولوژیکی می‌شود.با این حال الگوریتم ناسینوف از نظر تئوری در آموزش و پژوهش مورد توجه و علاقه است.برای مثال الگوریتم روش برگشت به عقب واترمن بایرز، Waterman-Byers-backtracking برای پیدا کردن زیرساختارهای بهینه به کار برده شد تا یک مثال از ماتریس برگشتی معین را توصیف کند. مطالعه الگوریتم آموزنده است، چرا که ، مانند الگوریتم‌های دیگر پیش‌بینی ساختار RNA، از روش برنامه‌نویسی پویا استفاده می‌کند که دارای یک ماتریس بازگشتی است و به آسانی قابل درک است.

• Stefan Wuchty, Walter Fontana, Ivo L. Hofacker, Peter Schuster: Complete Suboptimal Folding of RNA and the Stability of Secondary Structures. In: Biopolymers. 49, 1999, S. 145-165PDF, 317 KB

الگو

• Ruth Nussinov and George Pieczenik and Jerrold R. Griggs and Daniel J. Kleitman: Algorithms for Loop Matchings. In: SIAM Journal on Applied Mathematics. 35, Nr. 1, Juli 1978, S. 68-82.
• Durbin et al.: Biological sequence analysis. Cambridge, 2006, ISBN 0-521-62971-3, S. 269-272.